またぞろ三角関数の話

エッセンシャルワーカーは三角関数わからない的な言説をSNSでみた。う〜ん‥(わかるけど)使う機会少ないよね的な話なら多分そうなんでしょう。たしかに国会議員とか荷物を運搬するドライバーとか倉庫のフォーク作業で三角関数使う場面はないかもしれない。

ただこれ、自分は理解してるとSNSでドヤる人ほど(理系除き)多分わかってない。

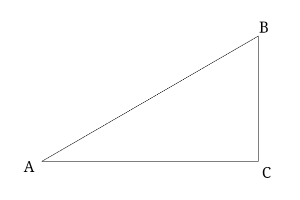
※ABC順序は作成ツールの仕様上こうなりました。

たとえば、C角を90とするABC直角三角形(斜辺AB隣辺AC対辺BC)でθ=A角30なら‥

対辺と斜辺の比は1:2つまり1/2
=(sin関数値)0.5000

隣辺と斜辺の比は√3:2つまり√3/2
【√3=1.73205080757】
1.73205080757÷2
=0.86602540378
=(cos関数値)0.8660

対辺と隣辺の比は1:√3つまり1/√3
【√3=1.73205080757】
1÷1.73205080757
=0.57735026918
=(tan関数値)0.5774

sin：斜辺を1と考えると‥
cos：斜辺を1と考えると‥
tan：隣辺を1と考えると‥

斜辺が100のときθ=A角30ならば対辺と斜辺の比は1:2つまり1/2=(関数値)0.5000と“言ってるんだから”対辺BCつまり高さは一意に50へ定まる。なるほど関数には違いない。

★なお三辺の比(三角比)はA角30の直角三角形なんで論理的にそうなる。

三角形の内角の和は180だから(内角が全て等しい)正三角形の対角頂点と対辺中点へ垂直二等分線を引けば論理的必然的に斜辺2対辺1の【比】をもつθ30の直角三角形をつくる。隣辺は【a²+b²=c²】で求められる。

つまりこう。
x²+1²=2²
x=√3

だが‥以上は【0<θ<90】に限定される説明なので、SNSなどでよく見る景色、自分⇆建物の距離と角度から高さを求める的な説明をしだす人、おそらく三角関数をわかってないと思う。わかってるなら最低限丶丶丶、xy平面の円単位上で定義されるsin、cos、tanから説明してほしい。三角関数で波について語ってほしい。三角関数は(理系除き)簡単じゃないし奥深いと思うけど、なんでSNS民って自分は余裕でござい‥て体をとるのかね。三角関数の微分とか極限とか逆三角関数の複素平面拡張とか本当に理解してるのか。